Hierarchical Table Order (Part I)

Version: 0.01.70 - last update: Wednesday, August 30, 2011, 14:35:00 (page links updated)

 

---

All you have to know about sorting table data hierarchically

Intro

When I implemented my first version of a native VFP TreeView control – just to see if it was feasible – I created the controlling driver table the typical “at least 2-columns” way. You still can download that outdated first try from here – just in case you want to peep at the table structure in question :-) After many, many hours of testing I found a couple of neat solutions to master all speed bottlenecks I encountered during test-driving my first VFP TreeView results. Today, I like to present to you one of the most interesting basics: how to sort a DBF-table hierarchically on only one column’s data WITHOUT loosing to much speed!!!

Hierarchical data - abstract

Some guys out here, even profs of computer sciences, claim that any set(s) of items can be organized hierarchically. Almost all taxonomies, numeric or non-numeric ones, have one thing in common: a one to many relationship between their members, spanning a tree-like structure stemming from one shared root element.

Hierarchies – concrete

Looking at objects at runtime, even during design-time while using “instance programming” in VFP, we immediately notice that any object has its unique identity and at least one reference path through which we can access its public members. Let’s have a look on a pretty common example showing how to print out the content of a VFP application’s textbox:

? m.goApp.oFormManager.Items(“AddressForm.1”).oPgfMaster.oPage1.oCntLeftPane.oTxtFirstName.Value

Nothing extravagant so far. So, what do we have here? There seems to be a public variable called “goApp” pointing to a global application object. Obviously, the application object contains some kind of form manager object, through which we can retrieve a form reference. In this case it is one of our address entry forms, from which a reference was stored in the form manager’s collection using a key value “AddressForm.1”. On this form there is a page frame oPgfMaster with a page oPage1 containing a VFP container object oCntLeftPane that holds the textbox oTxtFirstName we are looking for. Wow, finally we hold our textbox reference; from there we can print out the content of its value member. Well, I said it already, nothing special so far.

Let’s map this concrete implementation snapshot to the more abstract description: the root element of our reference path is our global reference m.goApp. From there we start walking the reference path down to our textbox object. There may be more than one textbox named oTxtFirstName in our application at the same time (especially if we’ve enabled multi-instance editing), but NOT inside the parent container named oCntLeftPane – the one that resides on oPage1 of oPgfMaster of .ITEM(“AddressForm.1”) managed by our app’s FormManager.
That said, everybody should understand what OBJECT IDENTITY is now. Every object has its own distinct and unique identity. In addition to that, as long as everything works flawlessly, there should be at least one reference path (like the one shown above) through which we are able to access each object individually. What we also see is, that the taxonomy tree spans from left to right. In other words, the one to many relations are written from left to right along the reference path: the form manager has many forms to manage, a form may contain more than one (top-level) page frame, a page frame usually has more than one page on it, and so on. Whereas every child can only belong to one parent at a time – at least, when it comes to real containment (in VFP). In other words: We cannot ADDOBJECT() a new class instance to more than one parental container object. In contrast to that, it is possible to add an object’s reference to more than only one other object through storing the reference to a property like so:

goApp.oCustomObjects.AddObject(“oMainForm”, “MyMainFormClass”) && add object into real container

loForm = goApp.oCustomizations.oMainForm && retrieve a local working copy of object reference

goApp.oFormManager.ADD(m.loForm, “AddressForm.1”) && a VFP collection is no container!

oApp.oSecurityManager.oMainForm = m.loForm && loose coupling only

and so on.
Line #4 shows how some security manager gets its main form reference. This reference assignment results only in loose coupling. This is no real containment-ship! Best proof: our main form has NO THIS.PARENT reference (to the security manager!) BTW, even when we use the ADD() method of the form manager collection, like shown on line #3 above, VFP internally does not establish a real containment there! VFP’s collection is no real container class but – well – a collection :-) Only on line #1 above, during instantiation, we added the form object to our custom container instance as a real child.

That said, we can recap that any VFP object reference used as a variable can be assigned many times to many different objects’ properties. In contrast to that, the object itself can only be instantiated once by another parent container class instance using ADDOBJECT() or NEWOBJECT(). I name this kind of parent objects (which references can be retrieved from within any child’s method using THIS.PARENT) the REAL PARENTS or short the CONTAINERS. All other objects holding references may only have some kind of logical parental relationship and therefor are called LOGICAL PARENTS! Again, there is no native support for logical parent-ship in VFP, only containment-ship is fully implemented!

A Short C# PEEK

.NET languages, like C#, don’t have neither functionality, nor class methods comparable to VFP’s THIS.ADDOBJECT() or THIS.NEWOBJECT(). You can instantiate any GUI control just the way you would do it in VFP with non-visual classes. Making a GUI control instance visible to the user is a simple act of adding the control’s reference to some form’s  controls collection. Simulating the procedure in VFP would look like so:

loTextBox = CREATEOBJECT(“MyTextboxClass”)
loMainForm.Controls.ADD(m.loTextBox)

In .NET every container has a controls collection – just like VFP – to which a child object (reference of a class instance) can be added dynamically.

Hierarchies – a General Approach

The only nice thing about long, descriptive reference names is, that most of the tokens we are using there are (more or less) easy to memorize. Even if I did not write the above code myself, I am still able to grasp the idea where to go to get the searched first name value. One of the downsides of descriptive names is that a computer program is not able to deal with the deeper sense transported with the names, like humans do. VFP tokenizes the names and stores them in an internal table (go and Google for VFP’s NTI – name table index entries). There is not much more you can do with them, but search for existence (e.g.  using PEMSTAT()). Well, you can setup a (complex) naming convention schema if you like but you have to write all of the necessary rule parsers and all the other weird stuff to enforce it on your own. Adding another semantic class to VFP’s variable- and property names introduce a whole new universe of troubles to solve.
Thus, my proposal is pretty different – I say: “Stop using object names!”

No, I do not mean “stop using names at all” but only in the first place! Let me show you how the textbox object’s value example above may be written within my FoxQuill framework:

? _GlobMem(“1.102.1.15.1.4.1.2.23.”).Value

Okay, you’re right, that looks pretty cryptic! But, using some custom intellisense functions make the whole thing as clear as any “verbose” name approach.  The idea behind my notation is, to substitute human readable reference names with a very simple to understand enumeration schema! These are my basic rules:

Every class instance (object) has a unique (running) number that makes it distinguishable from all other sibling objects at the same level (of containment).

Object numbering starts with <1>. (All <0>-based object references are reserved for internal use!)

All objects exactly have at least one logical parent. There can only be one start-point object that must not have any logical parent (the root).

The reference path to any object is written using n-dimensional array notation. (In VFP we have to use strings for that.)

Relation rule #1: Child numbers are written next to their logical parent IDs on the right side, separated by a dot.

Relation rule #2: Sibling objects have the same logical parent string and differ only in their own running number.

Let’s look at an example to make things a little bit clearer:
There’s a form with a container grouping a label and a textbox: oForm1.oCntFirstName.oLblFName and oForm1.ocntFirstName.oTxtFName

Let’s say that the form is the root object in this example. Then there are the following VECTOR expressions:

Form Vector	>>	“1.”
Container Vector	>>	“1.1.”
Label Vector	>>	“1.1.1.”
Textbox Vector	>>	“1.1.2.”

I named my “numbered reference paths” vectors. Every vector carries some implicit information:

It points to exactly one object, the so called endpoint object (the endpoint). Thus, it may be used as a unique identity descriptor for that endpoint!

It describes the parental hierarchy (the containment path) from the root to the endpoint.

Each number within a vector expression (separated by a dot) is called a dimension. Dimensions are enumerated from left to right.

The dot-count of a vector expression reflects the vector’s dimension width :=  lnDW = OCCURS(".", Vector)
      In our example above the textbox vector has an overall dimension width of <3>.

If we want to add a child to any object (even to non-containers!) we simply add the child to the object’s child dimension.

Let’s look at another example. Let’s say, we want to add some new controls to our form above. This was our form’s vector: “1.”
Now, let us add a PageFrame along with the existing container (at the same containment level). This is the vector expression of our new PageFrane: “1.2.”
Next, let us add three pages to the our PageFrane. These are the vector expressions of our new Pages: “1.2.1.”, “1.2.2.” and “1.2.3.”
Finally, let us add a container with another label and textbox to the 2nd page of our new PageFrane.
These are the corresponding vector expressions: “1.2.2.1.” (the container), “1.2.2.1.1.” (the label) and “1.2.2.1.2.” (the textbox).

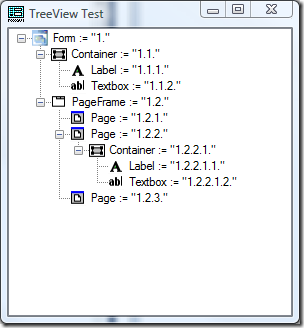
Now, the hierarchical object relations should look like in the image above. Naturally, we could have used named references as well:
? oForm.oPageFrame.oPage2.oContainer1.oTextBox1.Value is the same like this: ? oConstruct(“1.2.2.1.2.”) given that there is some collection-based object named oConstruct that holds a keyed reference to our textbox instance.

More to come

There are many more things to talk about when explaining “name-less” object reference constructions in-depth: how to maintain references using keyed collection, or how to organize (re-)numbering in case of object deletions. I will describe those different aspects pretty soon in later postings. We will talk about the so-called “zero-nodes” (e.g. “0.0.0.0.0.”), you will hear about a generic “inter-object messaging” system built into an object collection I named “the Matrix”). Finally, I will show you how simple otherwise complex object maintenance tasks can be realized if one uses a collection-based class instance storage (I named mine “the Construct”)… (“The blue or the red one, Nero?” ;-)

Hierarchical data – The Solution

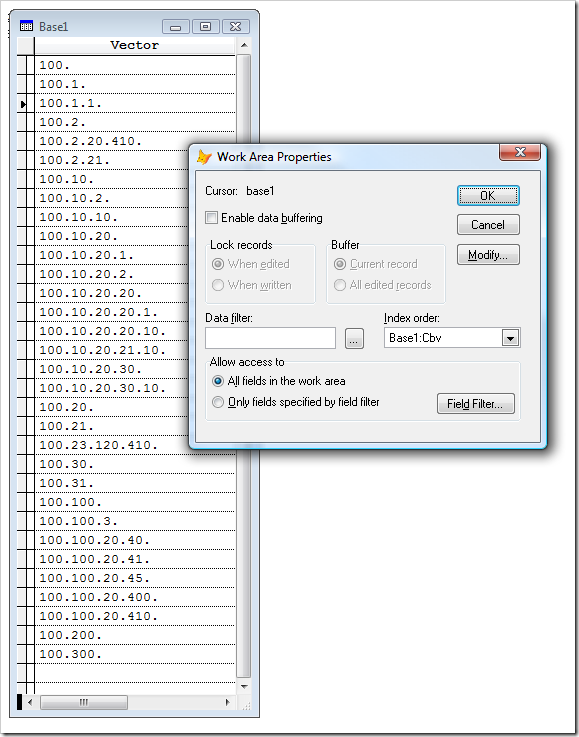
The screen shot above shows a TreeView which displays all items sorted correctly. Now, lets create a VFP free table to type in some test data. The outcome could look like the screen shot below:

At this early stage, the table has only one VARCHAR (binary) field called Vector which is 240 characters long. I like the VARCHAR field type, because there are no trailing blanks that have to be removed every time when fetching table data into memory. I think of VARCHAR as a regular CHAR field with an implicit RTRIM() functionality. BTW, be aware of the following: If you change a CHAR field to the VARCHAR field later, any data that has been already entered will retain its trailing spaces. An example: Maybe you have a table with a column named Clastname  (maybe a C(80) field). After 500 record were entered you decide to change your Clastname field to the new VARCHAR type V(80).  After that, another 500 address records were entered. Now, running through all 1000 records showing the effective content length of your Clastname field like so: ? LEN(Clastname) will show you, that the first 500 records all still print out > 80 <! Only the newly entered 500 records print their real “RTRIM()ed” varchar-lengths!

Thus, after changing an existing CHAR field containing data(!) to VARCHAR you should run a REPLACE ALL fieldname WITH ALLTRM(fieldname)ASAP!

The screenshot above shows us the non-ordered list of entries (their so-called chronological ordering). Now, lets add an index and activate it like so:

Adding a regular VFP index on the Vector column does not result in correct hierarchical sorting. As we can see, the records starting with “100.2.” should be sorted before those starting with  “100.10.”. Hierarchical data cannot be indexed using simple INDEX ON … commands without wrecking the correct hierarchical sort order. One way to overcome this would be to do a SORT TO <NewTable> for the whole table immediately after a change happened. This is absolutely impracticable! Another approach could be to use a refreshable view. Alas, REQUERIES  would become to slow, because the whole driving cursor has to be refreshed, even if only one record has been changed. What we need is something to generate an outcome like the following:

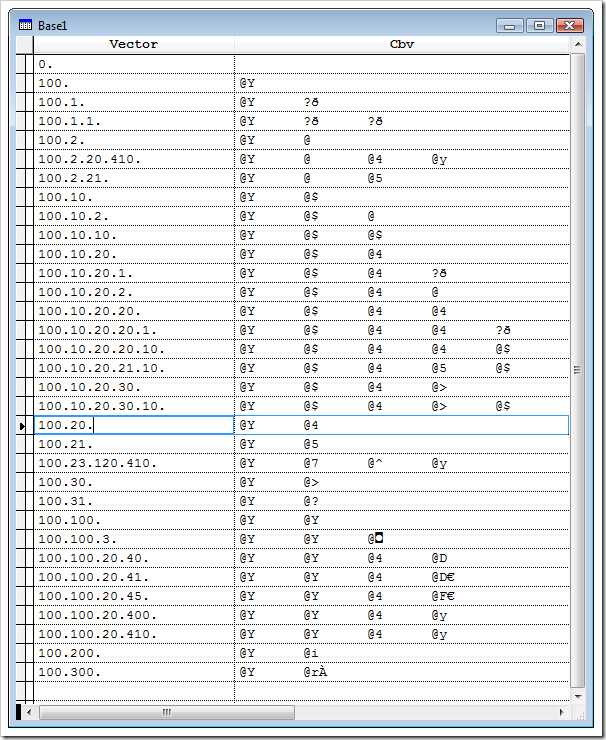
What is missing above is a second column that I named “Cbv” that holds the magic salt. BTW: the column/index name CBV stands for Compacted Binary View which describes the kind of data stored in that column. CBV-data can be indexed using a simple Visual FoxPro INDEX ON Cbv TAG ‘cbv’ command to solve all our hierarchical ordering problems!  

Before I show you the final implementation, here are some things one has to think about when dealing with VFP’s limited DBF-capacities: A CHAR field is limited in size to 254 (maximum), the size of a compound key is limited even more: 240 bytes is the maximum per index key, if the collating sequence is set to MACHINE.

We could argue that it is easy to retain the correct sort order. We only have to use dimension values with leading zeros like so:

000000100.000000000.000000000.000000000.

000000100.000000001.000000000.000000000.

000000100.000000002.000000020.000000410.

000000100.000000002.000000010.000000000.

000000100.000000003.000000000.000000000.

Well, that is absolutely right! But, how many dimensions do we need to allocate and how many items should then be provided within each dimension? One upper boundary is our 240 bytes we cannot exceed due to FoxPro’s index limitation. Thus, if we reserve 9 bytes for each dimension plus the dimension delimiting dot, we would end up using 10 bytes per dimension. That means, that we have 24 dimensions with enough address space to reference 999,999,999,999 items within each dimension. Seen from a capacity view point only, the dimensions seem huge enough. But, using our regular decimal system in combination with leading zeros that have to fill up every place throughout all used records generates more difficulties than it solves.
Fist of all, there is a huge performance hit when dealing with larger record sets. Imagine we have over 100,000 TreeView records; then a new TreeView item has to be added to a dimension which then will become the one with the highest dimension width (a new deepest TreeView nesting level will be reached). All existing 100,000 TreeView records have to be touched to add a new dummy set of “000000000.” to their existing string.

000000100.000000000.000000000.000000000.000000001. << adding  this one means:

000000100.000000001.000000000.000000000.000000000. << add dummies to all others!

000000100.000000002.000000020.000000410.000000000. << ditto.

000000100.000000002.000000010.000000000.000000000.<< ditto.

000000100.000000003.000000000.000000000.000000000.<< ditto.

Adding plus re-indexing renders this approach useless when running larger TreeViews. This technique is feasible only, if one is working with really small record sets, like in a Outlook scenario shown below:

Such kind of Outlook-style TreeViews are not used to display bulky data sets, but are employed for pure menu navigation purposes only! Thus, they are pretty much static, seen from the node count and ordering point of view.

The CBV Column

VFP brought us some cool functions and enhancements. Two of them are enhancements to the complementary CTOBIN() and BINTOC() functions. I do not want to re-type here what everyone can read in VFP’s help file about both function. Instead, I want to quote what is written in VFP’s help file in an additional chapter dealing with improved indexing support:

---

Create Small Indexes Using BINTOC( ) Sample

File: ...\Samples\Solution\Db\Index1.scx

This sample shows various indexing schemes you can use with numeric and integer data types to get significant savings in index size and disk space consumed. In addition, smaller sized indexes usually result in faster searches. The BINTOC() function makes it possible for you to convert an integer (numeric) value to a binary character representation.

Syntax

BINTOC(nExpression [, nSize])

Depending on the size of your expression, you can set the nSize parameter to accommodate the value of your expression in the least amount of characters.

The following line of code creates an index on a numeric field:

INDEX on line_no TAG line_no

The next time you are working with indexes on numeric integer data, consider using something like the following:

INDEX on BINTOC(line_no,1) TAG line_no

---

After playing with both functions for a while (BTW: there is a very informative demo under VFP’s Task Pane >> Solution Samples >> New in Visual FoxPro 9.0 >> BINTOC binary conversion) I started coding some routines to help me creating binary compacted string representations of the dimension values of my Vector column. The following listing takes a readable Vector expression like 454.42.753.146.8.1.77 and returns a CBV value that can be used for hierarchical indexing:

***---------------------------------------------------------------------------
*\\ Compact a "readable" VECTOR expression like 12.455.3.5566.1. into a
*\\ 	compressed binary vector string (with fixed dimension blocksizes!)
FUNCTION CompressVector(tcVector AS STRING, tnBlockSize AS Integer) AS STRING
	*\\ check input params
	IF NOT VARTYPE(m.tcValue) == "C" OR EMPTY(m.tcValue)
		RETURN "" && error condition
	ELSE
		*\\ Next line is necessary only if <tcVector>-data stems from a CHAR field 
		*** tcVector = ALLTRIM(m.tcVector)
		*//
	ENDIF
	*\\ let block size default to MAX_BLOCKSIZE
	IF NOT ( VARTYPE(m.tnBlockSize) == "N" AND INLIST(m.tnBlockSize, 4, 8) )
		tnBlockSize = MAX_BLOCKSIZE && MAX_BLOCKSIZE == 8 at the moment
	ENDIF
	*//
	LOCAL 	lnLoop AS INTEGER		,;	&& local loop variable
			lcNewVector AS STRING		&& local temprary string buffer			
	lcNewVector = ""
	*// define a symbol HSORT_SEPARATOR ”.”
	FOR lnLoop = 1 TO OCCURS(HSORT_SEPARATOR, m.tcVector)
		lcNewVector = m.lcNewVector + ;
			BINTOC(INT(VAL(GETWORDNUM(m.tcVector, m.lnLoop, HSORT_SEPARATOR))), "BRS")	
	NEXT
RETURN m.lcNewVector
ENDFUNC

The code I’m posting here is limited in that it allows only a fixed block size of 8 bytes at the moment. In other words, to save some extra bytes, I do not store dots between each dimension data any longer but use a fixed block size (of 8 bytes) instead. The final version will support 4 bytes and 2 bytes as well.  The rule of thumb is: The less block size each dimension occupies, the more dimensions can be used to nest hierarchical (e.g. TreeView-) items. The following screenshot shows you the second Cbv column filled with: REPLACE ALL Cbv WITH CompressVector(Vector) and then INDEX ON Cbv TAG ‘Cbv’. Setting the order to Cbv afterwards results in the sorted browse like shown below:

There are some other interesting side effects:
For instance, it is possible to drop the Vector column completely before starting digital delivery of your application. Okay, it is pretty easy to spot what kind of encryption is running behind the scenes. Anyway, there is no human readable numbering any longer, which is a better protection than none at all :-)
With a second retrieval function (I called mine “DeCompressVector”) it is also possible to recreate the Vector column values from the Cbv column values. You will find all functions below (at the end of this post).
Because the binary vector expressions are unique (due to the uniqueness of object identity) they can also be used as primary keys!

End of Part I

This is the the end of my first part showing you how to setup a table to get sorted hierarchically on one column only! Keep in mind that there will be more supporting functions which will help us maintaining TreeView driving tables using a binary vector column like shown above. The most common scenarios that need to be supported are:

Inserting one or more items (creating table rows with appropriate Cbv values).

Deleting item(s).

Moving item(s).

Reorganizing driving table (re-indexing).

Re-creating (readable) Vector column entries, in case they were dropped.

In addition to that there will be even more functions to support specific TreeView behavior like expanding/collapsing branches and other things.

 Happy coding

---

The X-Files

SET PROCEDURE TO (SYS(16)) ADDITIVE
RETURN

*\\ ***************** //* 
*** ***************** ***
*** HierachicSort.prg ***
*** ***************** ***
*// ***************** //*

#DEFINE HSORT_SEPARATOR "."
#DEFINE MAX_BLOCKSIZE 8

#IF .F. && ===================================================================
	MAX_BLOCKSIZE represents the maximum number of bytes it takes to
	compress one dimension value of a given VECTOR-Expression. At the moment
	(within Visual FoxPro) MAX_BLOCKSIZE MUST BE an 8 bytes Character expression 
	for CTOBIN() using "N.." as the 2nd parameter to work correctly. 
	The BlockSize setting is set for ALL Dimension. In other words: 
				One CANNOT mix 1, 2, 4 and 8 bit dimensions!

	The compact index (.cdx) we use for hierachial sorting has a maximum width 
	of 240 caracters. Thus, we can store vectors with up to 30 dimensions using
	an 8-bytes width (30 * 8 = 240) or 60 dimensions using a 4-bytes width
	accordingly. The highest scalar dimension value that can be compresses into 
	8 bytes is (15 places) which is 999,999,999,999,999 => 999 trillions!

	BTW: 
		9,007,199,254,740,992 is VFP's mamimum digits of precision in NUMERIC 
		computations (16 digits).

	In other words: At the moment we are able to handle VECTOR-Expression up to 
	30 dimensions with each dimension holding up to 999999999999999 possible 
	sub-dimensions or nodes!

#ENDIF && ===================================================================

***---------------------------------------------------------------------------
*\\ Compress a given string/numeric value
*\\ Parameter checking and function overloading
FUNCTION Compress(teValue AS VARIANT) AS STRING
	*\\ the largest <teValue> integer value is 999999999999999
	IF VARTYPE(m.teValue) == "N"
		IF m.teValue > 999999999999999
			*\\ error condition
			RETURN ""
		ELSE
			*\\ call implementation
			RETURN CompressNumber(m.teValue)		
		ENDIF
	ELSE
		IF VARTYPE(m.teValue) == "C" AND NOT EMPTY(m.teValue)
			*\\ the largest <teValue> string value is >999999999999999<
			IF m.teValue > "999999999999999"
				*\\ error condition
				RETURN ""
			ELSE
				*\\ call implementation
				RETURN CompressString(ALLTRIM(m.teValue))
			ENDIF
		ELSE
			*\\ error condition
			RETURN ""
		ENDIF
	ENDIF
ENDFUNC

***---------------------------------------------------------------------------
*\\ Compress a given string (compress() function overload#1)
FUNCTION CompressString(tcValue AS STRING) AS STRING
	*\\ Do the job w/o parameter testing
	RETURN BINTOC(INT(VAL(m.tcValue)), "BRS")
	*//
ENDFUNC

***---------------------------------------------------------------------------
*\\ Compress a given number (compress() function overload#2)
FUNCTION CompressNumber(tnValue AS NUMBER) AS STRING
	*\\ Do the job w/o parameter testing
	RETURN BINTOC(m.tnValue, "BRS")
	*//
ENDFUNC

***---------------------------------------------------------------------------
*\\ Decompress a given (compacted) binary string value
FUNCTION DeCompress(tcValue AS STRING, tnBlockSize AS Integer) AS STRING
	*\\ check input params
	IF NOT VARTYPE(m.tcValue) == "C" OR EMPTY(m.tcValue)
		RETURN "" && error condition
	ENDIF
	*\\ let block size default to MAX_BLOCKSIZE
	IF NOT ( VARTYPE(m.tnBlockSize) == "N" AND INLIST(m.tnBlockSize, 4, 8) )
		tnBlockSize = MAX_BLOCKSIZE && MAX_BLOCKSIZE always == 8 in VFP
	ENDIF
	*//
	IF LEN(m.tcValue) = m.tnBlockSize
		RETURN DeCompressValue(m.tcValue)
	ELSE
		IF LEN(m.tcValue) <= m.tnBlockSize
			RETURN DeCompressValue(PADR(m.tcValue, m.tnBlockSize, CHR(0)))
		ELSE
			RETURN DeCompressValue(LEFT(m.tcValue, m.tnBlockSize))
		ENDIF
	ENDIF
	*//
ENDFUNC

***---------------------------------------------------------------------------
*\\ Decompress() standard implementation
FUNCTION DeCompressValue(tcValue AS STRING) AS STRING
	*\\ parameter checking is done in ExpandValue()
	RETURN TRANSFORM(INT(CTOBIN(m.tcValue, "NRS")))
	*//
ENDFUNC

***---------------------------------------------------------------------------
*\\ Compact a "readable" VECTOR expression like 12.455.3.5566.1. into a
*\\ 	compressed binary vector string (with fixed dimension blocksizes!)
FUNCTION CompressVector(tcVector AS STRING, tnBlockSize AS Integer) AS STRING
	*\\ check input params
	IF NOT VARTYPE(m.tcValue) == "C" OR EMPTY(m.tcValue)
		RETURN "" && error condition
	ELSE
		*\\ Next line is necessary only if <tcVector>-data stems from a CHAR field 
		*** tcVector = ALLTRIM(m.tcVector)
		*//
	ENDIF
	*\\ let block size default to MAX_BLOCKSIZE
	IF NOT ( VARTYPE(m.tnBlockSize) == "N" AND INLIST(m.tnBlockSize, 4, 8) )
		tnBlockSize = MAX_BLOCKSIZE && MAX_BLOCKSIZE always == 8 in VFP
	ENDIF
	*//
	LOCAL 	lnLoop AS INTEGER		,;	&& local loop variable
			lcNewVector AS STRING		&& local temprary string buffer			
	lcNewVector = ""
	*//
	FOR lnLoop = 1 TO OCCURS(HSORT_SEPARATOR, m.tcVector)
		lcNewVector = m.lcNewVector + ;
			BINTOC(INT(VAL(GETWORDNUM(m.tcVector, m.lnLoop, HSORT_SEPARATOR))), "BRS")	
	NEXT
RETURN m.lcNewVector && + "."
ENDFUNC

***---------------------------------------------------------------------------
*\\ Expand a compressed (binary) VECTOR string into a "readable" VECTOR
*\\ 	expression like 12.455.3.5566.1.
FUNCTION DeCompressVector(tcExpression AS STRING, tnBlockSize AS Integer) AS STRING
	*\\ check input params
	IF NOT VARTYPE(m.tcExpression) == "C" OR EMPTY(m.tcExpression)
		RETURN "" && error condition
	ENDIF
	*\\ default block size to max block size
	IF NOT ( VARTYPE(m.tnBlockSize) == "N" AND INLIST(m.tnBlockSize, 4, 8) )
		tnBlockSize = MAX_BLOCKSIZE && MAX_BLOCKSIZE is always 8 in VFP
	ENDIF
	*//
	LOCAL 	lnLoop AS INTEGER		,;	&& local loop variable
			lcNewVector AS STRING		&& local temprary string buffer
	lcNewVector = ""
	*//
	FOR lnLoop = 0 TO ( LEN(tcExpression) / m.tnBlockSize ) - 1		
		m.lcValue =	SUBSTR(m.tcExpression, m.lnLoop * m.tnBlockSize + 1, m.tnBlockSize)
		lcNewVector = m.lcNewVector + ;
				TRANSFORM(INT(CTOBIN( 						;
				SUBSTR(m.tcExpression, m.lnLoop * m.tnBlockSize + 1, m.tnBlockSize),;
				"NRS"))) + "."
	NEXT
RETURN m.lcNewVector
ENDFUNC

---